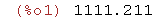
(%i1) 123.56+987.651;

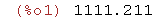
Podemos sumar números decimales.

Podemos calcular raíces cuadradas.

(%i2) sqrt(2);

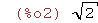
La expresión anterior no calcula una aproximación decimal
de la raíz cuadrada de 2.

Se trata la raíz cuadrada (positiva) de 2 como un número positivo
cuyo cuadrado es 2.

Sin embargo:

(%i3) sqrt(2.0);

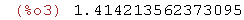
Es una aproximación decimal (con 15 decimales) de la raíz cuadrada de 2.

(%i4) sqrt(2)^2;

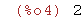
(%i5) sqrt(3); 3*sqrt(3)^2-sqrt(2);

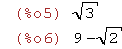
(%i7) sqrt(64);

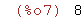
Así pues sqrt(2) es un símbolo que representa un número real positivo (el único),
cuyo cuadrado es 2.

Algo similar ocurre con el símbolo %i, que representa la unidad imaginaria. Es decir, un número
complejo cuyo cuadrado es -1.

(%i8) %i; %i^2; 1+2*%i; %i^3; %i^4;

También podemos simplificar expresiones "complicadas"

(%i13) (1+3*(4-6))/(8+3*(2-3*4));

Y multiplicar números (enteros o decimales) "grandes"

(%i14) 123456789000987654321*987654321000123456789;

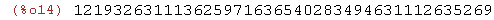
123456789.00123*2233445566778899.00112233;

(%i15) 123456789.00123*2233445566778899.00112233;

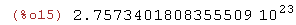
(%i16) sqrt(123456789);

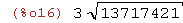
(%i17) sqrt(123456789.0);

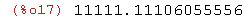
También podemos factorizar números enteros

(%i18) factor(123456789);

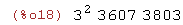
Incluso números enteros "grandes"

(%i19) factor(123456789876543212345678987654321);

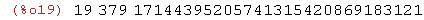
(%i20) 17144395205741315420869183121*19*379;

Pero ¡atención! la factorización de un número "grande" puede llevar miles de millones de años
al ordenador más potente del mundo ... (con los algoritmos de factorización actualmente conocidos).

Por ejemplo, no se conoce -a día de hoy- la factorización de este número (llamado
RSA-704):
740375634795617128280467960974295731425931888892312890849362326389727
650340282662768919964196251178439958943305021275853701189680982867331
732731089309005525051168770632990723963807867100860969625379346505637
96359

Tiene 212 cifras.

Relación con RSA y el comercio electrónico.

Factorizar el factorial de un número (posiblemente muy grande) es fácil.

Por ejemplo, 1000! tiene más de 2500 cifras!

(%i21) factor(1000!);