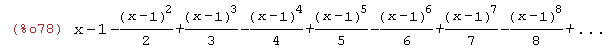Maxima manipula polinomios como objetos simbólicos.

Tiene implementada la aritmética de los polinomios.

(%i40) 2*x+3*x^3;

(%i41) 3*x^3-5*x^3+x+1;

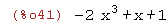
(%i42) (x+1)^2;

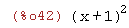
Un ejemplo de "evaluación perezosa" ("lazy evaluation")

(%i43) (x+1)^2-x^2;

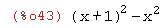
(%i44) expand((x+1)^2);

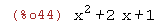
(%i45) expand((x+1)^2-x^2);

(%i46) factor(expand(x+1)^2);

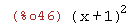
(%i47) x^3/x^2;

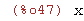
(%i48) (x-1)^3/(x-1);

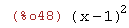
(%i49) (a*x+1)^2/(a*x+1);

(%i50) (a*x+1)^2/(b*x+1);

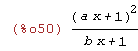
(%i51) (2*x^2+4*x^3)*(x^5+x+1);

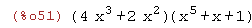
Otro ejemplo de "evaluación perezosa"

(%i52) expand((2*x^2+4*x^3)*(x^5+x+1));

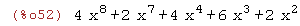
(%i53) %;

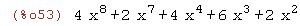
(%i54) factor(%);

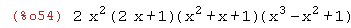
Nótese que el símbolo % tiene como valor el de la última expresión evaludada.

Además %oN es un símbolo que tiene como valor el resultado de la evaluación
de la línea de comandos %iN (aquí N es un número entero mayor o igual que 1).

(%i55) %o14;

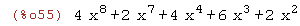
(%i56) %;

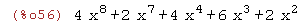
(%i57) 1/x+2*x/(x+1);

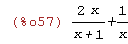
(%i58) ratsimp(1/x+2*x/(x+1));

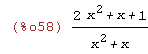
(%i59) expand(%);

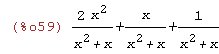
(%i60) rat(%);

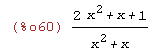
(%i61) gcd((x+1)*x^2, 2*x);

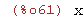
(%i62) gcd(24,2);

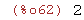
(%i63) lcm(3,5);

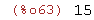
(%i64) lcm(3*x, 5*(x+1));

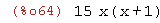
(%i65) lcm(3*x^2+5*x^4+x, 4*x+2*x^3+x);

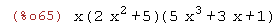
(%i66) gcd(3*x^2+5*x^4+x, 4*x+2*x^3+x);

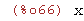
(%i67) divide(2*x^2+1,x);

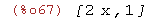
(%i68) A:divide(2*x^4+x^3+x+1,3*x^2+1);

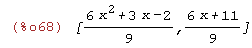
(%i69) expand(A[1]*(3*x^2+1)+ A[2]);

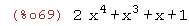
(%i70) A[1]; A[2];

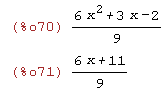
Nótese la sintaxis A: expresion

A[1] (el cociente) y

A[2] (el resto)

(%i72) remainder(2*x^4+x^3+x+1,3*x^2+1);

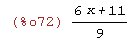
(%i73) quotient(2*x^4+x^3+x+1,3*x^2+1);

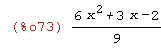
Sobre el algoritmo de "ordenación" de las expresiones evaluadas

(%i74) 1/x^2+(x+1)/x+1/x;

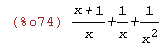
Otro ejemplo de "evaluación perezosa" ...

(%i75) taylor(sin(x),x,0,10);

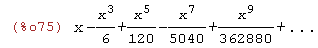
(%i76) taylor(sin(x),x,0,20);

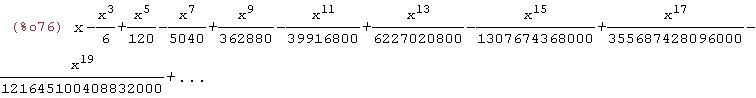
(%i77) taylor(log(x),x,0,3);

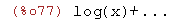
(%i78) taylor(log(x),x,1,8);