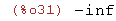(%i1) example(limit);

Cálculo de límites

(%i6) limit((x+1)/(2*x),x,inf);

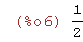
(%i7) limit((x+1)/(2*x),x,0);

(%i8) limit(sin(x),x,inf);

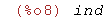
(%i9) limit(log(x),x,0,plus);

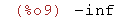
(%i10) log(%e);

log(x) es el logaritmo neperiano de x

¿Y las funciones logaritmos en otras bases?

(%i11) wxplot2d([log(x)], [x,-1,5],
 [gnuplot_preamble, "set grid;"])$

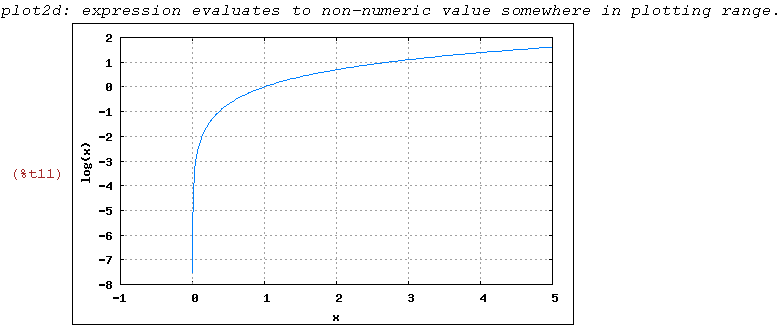
Pero cuidado

(%i12) limit(log(x),x,0);

¿Tiene la fórmula anterior alguna explicación?

(%i13) limit(sqrt(x),x,0);

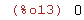
(%i14) limit(sqrt(-x),x,0);

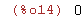
Límite en el dominio de los números complejos

(%i15) limit(sqrt(x),x,-1);

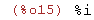
(%i16) limit((x^2-1)/(x^2-4*x+3), x, 1);

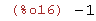
(%i17) limit(sqrt(x^2+x)-sqrt(x^2-3*x),x,inf);

(%i18) (sqrt(x^2+x)-sqrt(x^2-3*x))*(sqrt(x^2+x)+sqrt(x^2-3*x));

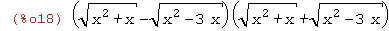
(%i19) ratsimp((sqrt(x^2+x)-sqrt(x^2-3*x))*(sqrt(x^2+x)+sqrt(x^2-3*x)));

(%i20) 4*x/(sqrt(x^2+x)+sqrt(x^2-3*x));

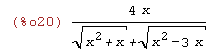
(%i21) limit(sin(2*x)/x,x,0);

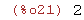
(%i22) limit(sin(-2*x)/x,x,0);

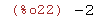
(%i23) limit(sin(a*x)/x,x,0);

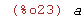
Atención al uso del infinito

(%i24) limit(cos(x)/x,x,0);

(%i25) limit(cos(x)/sin(x),x,0);

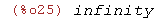
(%i26) limit(cos(x)/sin(x),x,0,plus);

(%i27) limit(cos(x)/sin(x),x,0,minus);

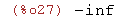
(%i28) limit(x^2/(x-1), x, 0);

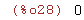
(%i29) limit(x^2/(x-1),x,1);

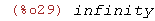
(%i30) limit(x^2/(x-1),x,1,plus);

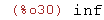
(%i31) limit(x^2/(x-1),x,1,minus);