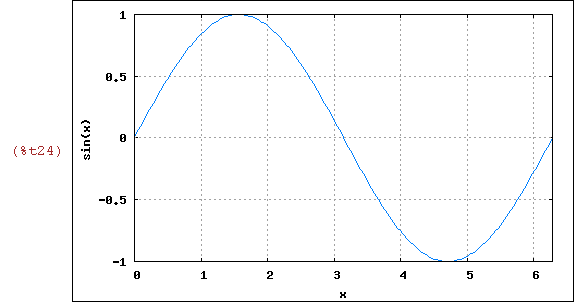
(%i24) wxplot2d([sin(x)], [x,0,2*%pi],
 [gnuplot_preamble, "set grid;"],
 [nticks,12])$

Se puede usar el desplegable "Gráficos 2D" y después modificar
plot2d a wxplot2d

Nótese que la constante Pi se denota %pi

(%i25) %pi; float(%pi);

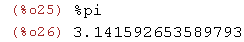
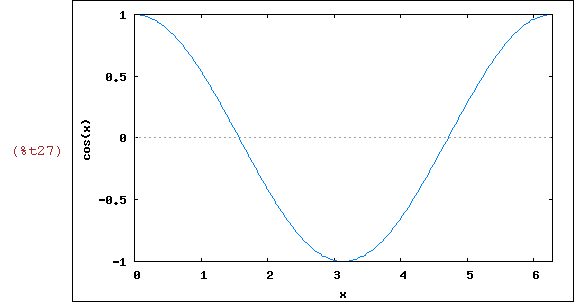
(%i27) wxplot2d([cos(x)], [x,0,2*%pi])$

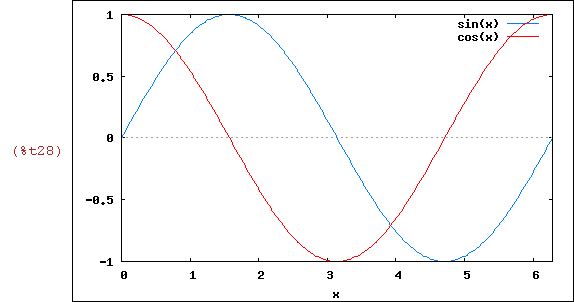
(%i28) wxplot2d([sin(x),cos(x)], [x,0,2*%pi])$

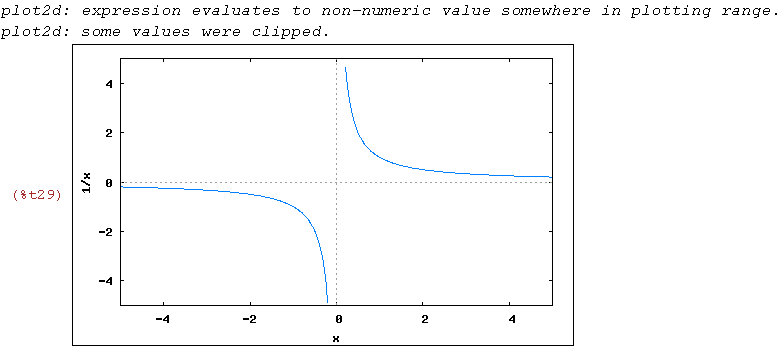
(%i29) wxplot2d([1/x], [x,-5,5], [y,-5,5])$

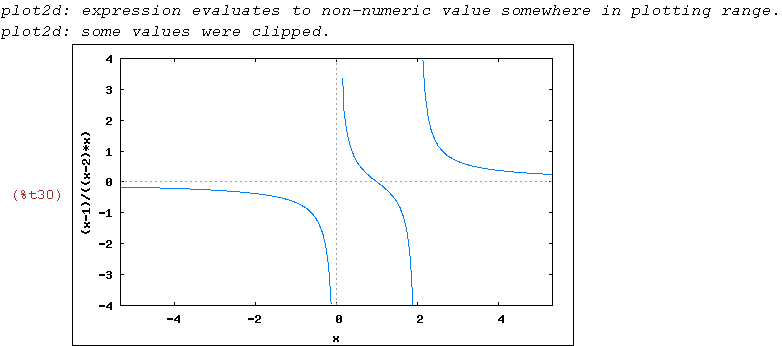
(%i30) wxplot2d([(x-1)/(x*(x-2))], [x,-16/3,16/3],[y,-4,4])$

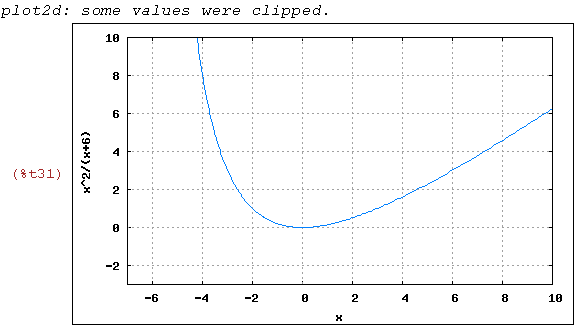
(%i31) wxplot2d([x^2/(x+6)], [x,-7,10],[y,-3,10],
 [plot_format, openmath],
 [gnuplot_preamble, "set grid;"])$

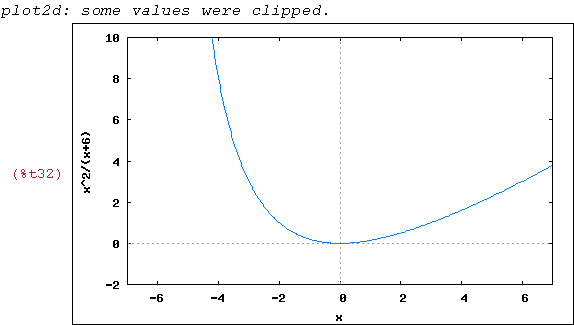
(%i32) wxplot2d([x^2/(x+6)], [x,-7,7],[y,-2,10])$

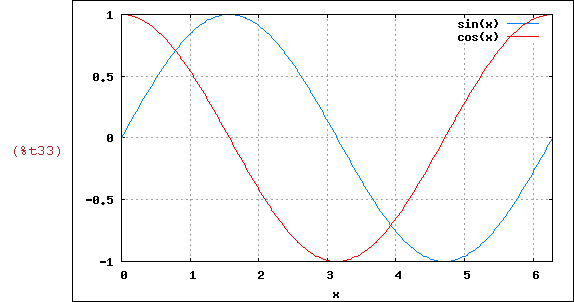
(%i33) wxplot2d([sin(x),cos(x)], [x,0,2*%pi],
 [gnuplot_preamble, "set grid;"])$

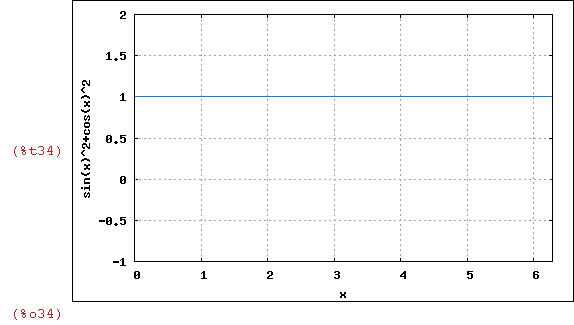
(%i34) wxplot2d([(sin(x))^2+(cos(x))^2], [x,0,2*%pi],[y,-1,2],
 [gnuplot_preamble, "set grid;"]);

(%i35) wxplot2d(%e^x, [x,-5,5],[y,-2,10],
 [gnuplot_preamble, "set grid;"]);

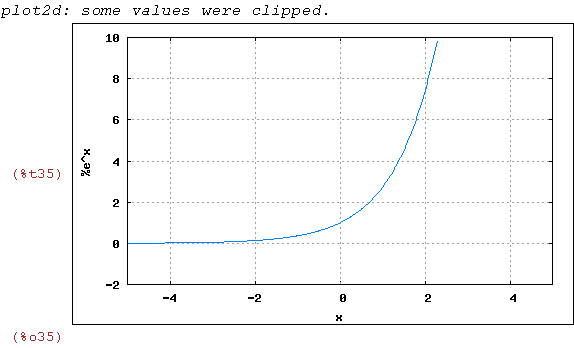
Nótese que la constante e (base de los logaritmos neperianos) se denota %e

La unidad imaginaria se denota %i

(%i36) %i^2;

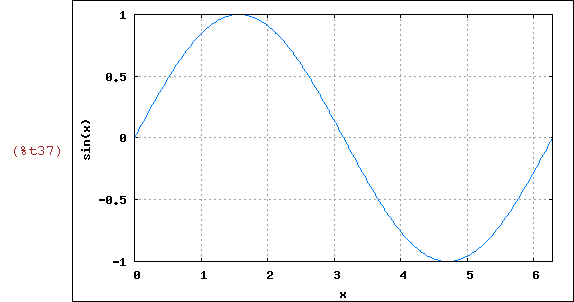
(%i37) wxplot2d([sin(x)], [x,0,2*%pi],
 [gnuplot_preamble, "set grid;"])$

-->

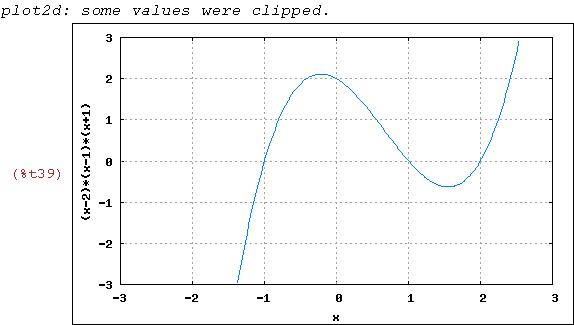
(%i39) wxplot2d([(x+1)*(x-1)*(x-2)], [x,-3,3],[y,-3,3],
 [gnuplot_preamble, "set grid;"])$

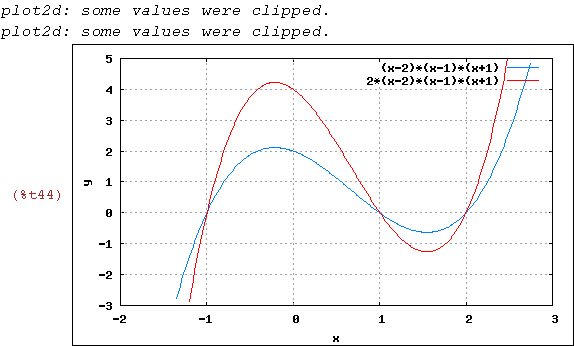
(%i44) wxplot2d([(x+1)*(x-1)*(x-2),2*(x+1)*(x-1)*(x-2)], [x,-2,3],[y,-3,5],
 [gnuplot_preamble, "set grid;"])$